2025 Summer School on Combinatorics and Algorithms

- Date: 14-18 July 2025.
- Place: POSTECH.
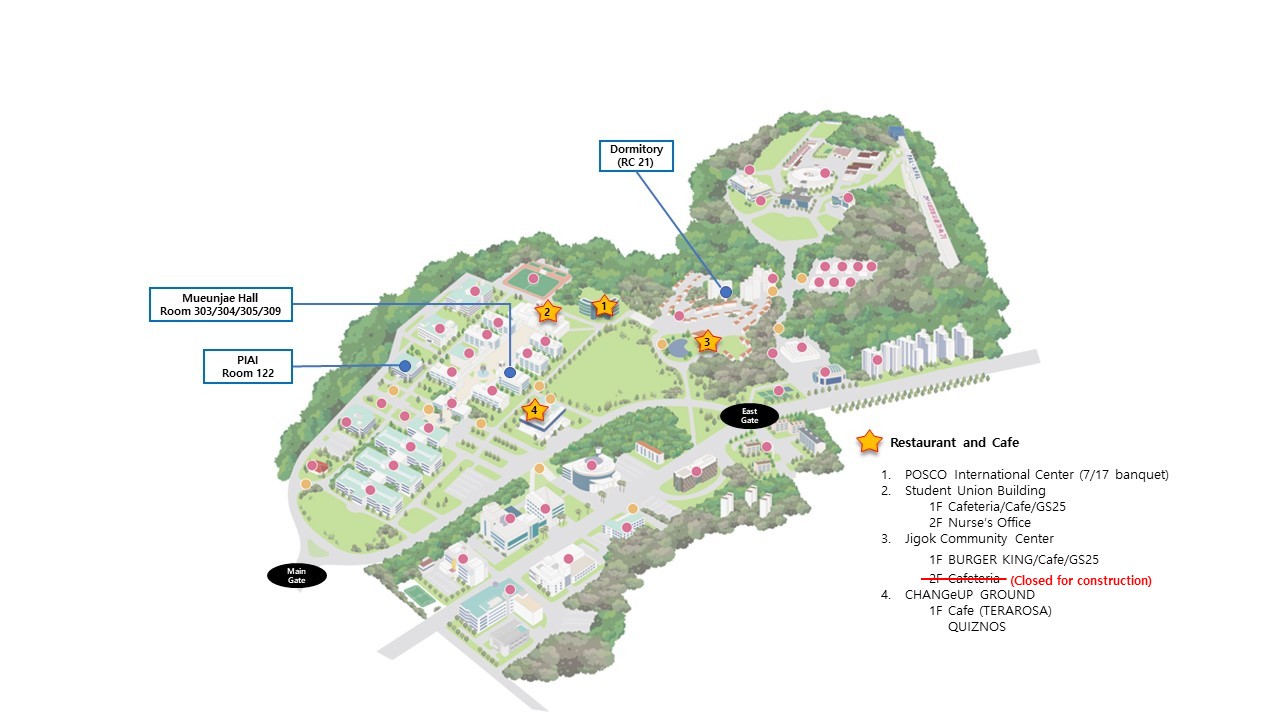
- Lecture: 1 Institute of Artificial Intelligence (인공지능연구원) Room 122
- Group Discussion and Recitation: 3 Engineering Building II, Room 104 (Group 1~4), Room 106 (Group 5~8), Room 107 (Group 9~12), Room 109 (Group 13~16)
- Free Discussion in the Evening: 2 Hogil Kim Memorial Hall (무은재기념관) Rooms 303, 304, 305, 309
The 2025 Summer School on Combinatorics and Algorithms is a venue for students and early-career researchers to learn selected topics in theoretical computer science and discrete mathematics. It will be a great opportunity for young and aspiring researchers to study topics which are important but not covered during the lectures in the university classes.
Lecturers and Topics

Édouard Bonnet
LIP, CNRS.
Induced Subgraphs and Induced Minors of Graphs
In graph theory, the notion of minor extends that of subgraph by further allowing edge contractions. There is a deep and beautiful theory of graph minors, initiated and mainly carried out by Robertson and Seymour in the Graph Minors Project. Among the remarkable results, we find the following theorems.
-
There exists a function f such that every graph of treewidth at least f(k) contains a k × k grid as a minor, or a subdivision of a k × k wall as a subgraph.
-
Every class excluding a planar graph as a minor has bounded treewidth.
-
Graphs excluding a fixed minor H can be “decomposed” into graphs that are “almost embeddable” on surfaces of bounded genus (Robertson and Seymour’s structure theorem).
-
The relation “being a minor of” is a well-quasi-order on the class of all finite graphs.
-
For every class 𝒞 excluding a fixed minor, the n-vertex graphs in 𝒞 have treewidth O(√n).
These facts have interesting algorithmic onsequences. In classes excluding a fixed graph as a minor, most problems can be solved faster or approximated better than on general graphs. However, even the simplest dense class, the class of all complete graphs, does not exclude any graph as a minor. This is because edge deletions are allowed in the definition of minor. What if we disallow them? We then get the notion of induced minor.
This class revisits all the above facts for induced minors. This is a developing theory, about five years old, with a few positive results and must-know constructions, and several exciting conjectures.

Michał Pilipczuk
University of Warsaw.
Structural Theory of Sparse Graphs
What does it mean for a graph to be sparse? The answer to this innocently looking question turns out to be not so obvious: depending on the point of view, different concepts of sparsity can be studied. We will take a deeper dive into a particular angle on this topic, introduced around 2008 by Nešetřil and Ossona de Mendez. They proposed to measure the density of local structures that can be found in graphs: the so-called shallow minors. This point of view leads to two natural definitions — of graph classes of bounded expansion and of nowhere dense graph classes — that capture the idea of uniform sparsity visible at a local level. It turns out that both notions admit multiple different combinatorial characterizations, each presenting a different facet of the concept and providing a technique for working with sparse graphs. The emerging net of relationships became a research area called Sparsity. Apart from a myriad of graph-theoretic tools, the area also offers a number of algorithmic applications and has intricate connections with finite model theory.
During the lectures and tutorials, we will give a broad introduction to Sparsity. Below is a tentative range of topics that will be covered:
- Measuring sparsity: Shallow (topological) minors and measuring sparsity using them. Concepts of bounded expansion and nowhere denseness.
- Structural characterizations: Generalized coloring numbers, treedepth and low treedepth coverings and their relation with bounded expansion and nowhere denseness. Combinatorial and algorithmic applications.
- Characterizations of nowhere denseness: flatness (aka uniform quasi-wideness) and Splitter game.
- Outlook on the model-theoretic structure theory for dense graphs: transductions, monadic stability, monadic dependence, flip-flatness and Flipper games.
Schedule
- Start on 14 July 2025 Monday, 2 PM
- Registration and Entry Badge Collection
- Time: July 14 (Mon), 12:00 PM – 1:30 PM
- Location: Room 122, 1st Floor, PIAI building
- Please wear your entry badge at all times during the event and return it at the same location on the last day.
- Banquet: Thursday evening, July 17, at the POSCO International Center.
- End on 18 July 2025 Friday, 5 PM
| Monday | Tuesday | Wednesday | Thursday | Friday | ||
| 9:00 | 9:00 | |||||
| 9:15 | 9:15 | |||||
| 9:30 | Bus from IBS, Daejeo | Lecture A2 | Lecture A4 | Leccture A6 | Lecture A8 | 9:30 |
| 9:45 | to Pohang | 9:45 | ||||
| 10:00 | 10:00 | |||||
| 10:15 | 10:15 | |||||
| 10:30 | 10:30 | |||||
| 10:45 | Lecture B2 | Lecture B4 | Lecture B6 | Lecture B8 | 10:45 | |
| 11:00 | 11:00 | |||||
| 11:15 | 11:15 | |||||
| 11:30 | 11:30 | |||||
| 11:45 | 11:45 | |||||
| 12:00 | 12:00 | |||||
| 12:15 | 12:15 | |||||
| 12:30 | 12:30 | |||||
| 12:45 | 12:45 | |||||
| 13:00 | 13:00 | |||||
| 13:15 | 13:15 | |||||
| 13:30 | Lecture A3 | Lecture A5 | Lecture A7 | Recitation | 13:30 | |
| 13:45 | 13:45 | |||||
| 14:00 | Welcome | 14:00 | ||||
| 14:15 | Lecture A1 | 14:15 | ||||
| 14:30 | 14:30 | |||||
| 14:45 | Lecture B3 | Lecture B5 | Lecture B6 | Lecture A9 | 14:45 | |
| 15:00 | 15:00 | |||||
| 15:15 | 15:15 | |||||
| 15:30 | 15:30 | |||||
| 15:45 | 15:45 | |||||
| 16:00 | Lecture B1 | Group Discussion | Group Discussion | Group Discussion | Lecture B9 | 16:00 |
| 16:15 | 16:15 | |||||
| 16:30 | 16:30 | |||||
| 16:45 | 16:45 | |||||
| 17:00 | Recitation | Recitation | Recitation | 17:00 | ||
| 17:15 | 17:15 | |||||
| 17:30 | Check-in to the Dorm | Bus from Pohang | 17:30 | |||
| 17:45 | to IBS, Daejeon | 17:45 | ||||
| 18:00 | 18:00 | |||||
| Banquet | ||||||
Registration
- Register at https://indico.ibs.re.kr/e/combialgo2025: Deadline May 31.
Organizers
- Eunjung Kim (KAIST School of Computing)
- Sang-il Oum (IBS Discrete Mathematics Group)
- Eunjin Oh (POSTECH CSE)
History
Local Information